United We Stand
Raghav Arora
May 26, 2020
Millions of years of evolution has taught us the value of living and working in groups. To ensure their survival, our ancestors hunted in groups and lived in communities. Over time, more and more people joined such communities, which resulted in the rise of towns and cities we see today. This phenomenon is observed not only in humans, but also in animals - elephants, lions, wolves, bees, and ants are often seen in packs.
Such coalitions are everywhere around us - labor unions exist all over the world and taxi mafias operate in every tourist hotspot. As a matter of fact, we inadvertently form coalitions everyday.
Most of us work in an organization, which essentially is a coalition that enables us to create more value together than we would when working independently.
On taking a bus to work instead of a car, we form a coalition with other passengers in the bus to reduce per person transportation costs.
Neighbors form coalitions by way of homeowner associations that ensure the upkeep of the neighborhood, which helps maintain high rents and property values.
Models of cooperation are not limited to just friendly players and rivals can often be seen working together to accomplish something they cannot on their own.
In November 2018, competing automakers Tesla, GM and Nissan joined forces to form the EV Drive Coalition in an effort to lobby US lawmakers for the extension of the $7,500 per-vehicle consumer tax credit that incentivizes customers to buy electric vehicles.
In the 2019 Canadian federal election, Justin Trudeau retained his position as the Prime Minister, but the Liberal Party of Canada failed to secure a majority win. This means that to pass any new legislation now, the liberals need other members of the parliament to cooperate with them. It also means that the other parties can form a coalition to vote on an opposition motion that the liberals may not be comfortable with, as can be seen in the following vote counts
Creating coalitions is natural human behavior and some concepts of behavioral economics can be used to answer some fundamentals such as
How coalitions form in a game of self-interested players?
What is the total worth of a coalition?
What are the individual payoffs of the members in a coalition?
Who is the most valuable player in a coalitional game?
Coalitional Game Theory
Coalitional Game Theory is the branch of behavioral economics that explores the idea that subsets of players in a game can form a “cartel” and act in unison to gain more than they would if they acted independently. Such cartels are termed as coalitions.
Games of Coalition
A Coalitional Game with Transferable Utility is a game in which players can cooperate with each other to maximize their combined payoff, which can be redistributed among themselves.
Mathematically, it can be defined as a pair (N, v), where N is a finite set of players, and v is a characteristic function that maps each coalition S ⊆ N to its worth v(S), which is a real-valued payoff that the coalition’s members can distribute among themselves. We assume that v(∅) = 0.
Car pooling, labor unions and cartels are some good examples of coalitional games.
Nalebuff’s Taxi Ride
Barry Nalebuff explains a simple example of car pooling that can be used to study coalitional games.
3 coworkers Alice, Bob and Carol who leave the office at the same time, live in different parts of the city. The taxi fare for them to go home is $6, $11, and $15 respectively.

They look at the map of taxi-fares above and decide to save money by sharing the taxi. In the coalition (A,B,C), the group spends $18 in total by taking route origin - A - B - C. Going separate ways would have cost them $6, $11 and $15 respectively and they would have spent a total of $32. By sharing the taxi, they save $14.
Calculating Shapley Values
To understand Shapley values, turn to last week’s issue of the The Tinkerer, where I explained the significance of Shapley values and how they can be used to determine the fair division of payoffs in a game of cooperation.
To split the costs fairly among each player, we look at their Shapley values, which can be calculated by averaging over every order, the marginal contributions of Alice, Bob and Carol towards a total fare of $18.
Infeasible routes The order of dropping Alice, Bob and Carol will always be ABC, which costs $18. ABC is the most economical route and every other route entails a higher cost and is therefore infeasible
Consider the order ABC
The route for Alice is Origin - A, which costs $6. Alice pays $6.
Bob joins Alice to form a coalition and now the new route is Origin - A - B, which costs a total of $12. Bob only pays his marginal contribution of $6 as Alice has already paid $6 towards the taxi fare.
Carol joins the coalition and now the new route is Origin - A - B - C, which costs a total of $18. Carol only pays her marginal contribution of $6 as Alice and Bob have already paid $12 towards the taxi fare.
Similarly, for the order CAB
The route for Carol is Origin - C, which costs $15. Carol pays $15.
Alice joins Carol to form a coalition and now the new route is Origin - A - C, which costs a total of $17. Alice only pays her marginal contribution of $2 as Carol has already paid $15 towards the taxi fare.
Bob joins the coalition and now the new route is Origin - A - B - C, which costs a total of $18. Bob only pays his marginal contribution of $1 as Alice and Carol have already paid $17 towards the taxi fare.
Similarly, for all orderings, the marginal contribution of each player and the corresponding Shapley values are as follows
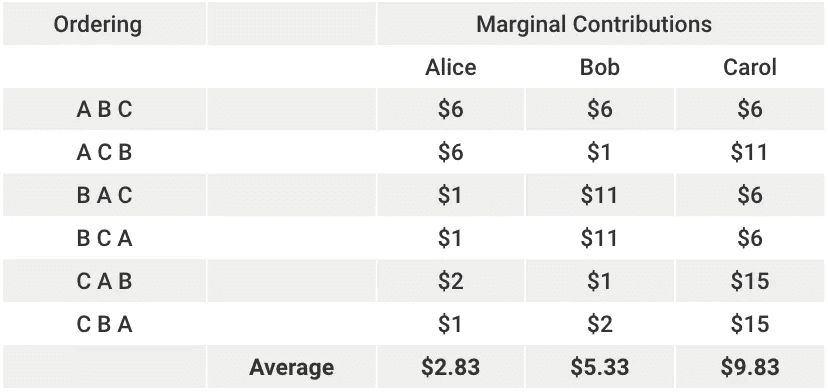
The fair split comes out to be $2.83 for Alice, $5.33 for Bob and $9.83 for Carol, and everyone in the coalition saves a considerable amount of money.
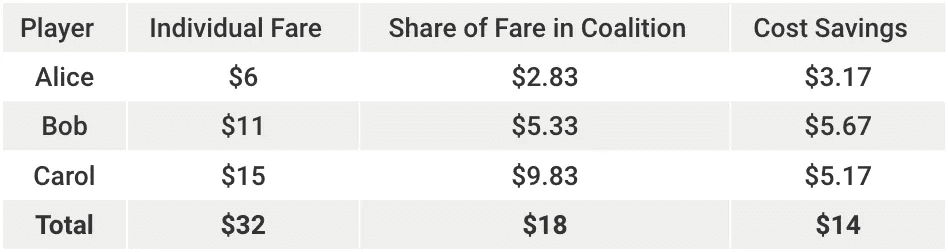
On forming the grand coalition, the group saves a total of $14 in costs and every player benefited from sharing the taxi. The worth of the grand coalition comes out to be $14 and the individual payoffs of each player are their respective cost savings.
A coalition that consists of each and every player in a game is called the grand coalition
The MVP
It is interesting to note that Bob saves almost $6 while Alice only saves about $3. To understand why there exists such a difference, consider the sub-coalitions (A,B), (B,C), and (A,C).
When only Alice and Bob share the taxi, they spend $12. Going separately would have cost them a total of $17. By forming this coalition, they save $5.
When only Bob and Carol share the taxi, they spend $17. Going separately would have cost them a total of $26. By forming this coalition, they save $9.
When only Alice and Carol share the taxi, they spend $17. Going separately would have cost them a total of $21. By forming this coalition, they save $4.
Absent of the option of a grand coalition, the cost-savings for the sub-coalitions are in the order (A,C) < (A,B) < (B,C)
Alice would prefer to create a coalition with Bob over Carol
Bob would prefer to create a coalition with Carol over Alice
Carol would prefer to create a coalition with Bob over Alice
It is clear that Bob brings the most value to the coalition and thus is the most valuable player (MVP) of this game. In contrast, Alice brings the least value to the coalition. This is also reflected in the fair split determined by the Shapley value.
Coalitions and Business
Coalitional Game Theory has some obvious applications in business and entrepreneurship. Here are some examples that come to mind
Uber, Lyft and other ride hailing services can engineer a much needed revenue boost by optimizing their ride-share algorithms using these calculations.
Zomato, DoorDash and similar food delivery services can apply these calculations to plan faster and more cost-efficient delivery routes.
Airlines can leverage coalitional game theory to assess strategic partnerships which would allow them to service new routes.
Organizations can check for possible flaws in their business model such as determining whether customers will form groups to exploit their services (sharing access to netflix, udemy, kindle, etc.)
If you found this week’s post useful, I would love to talk to you about your plan on leveraging these ideas. You can reach out to me on twitter or just reply to this email.
Further Readings