Stick to the Core

In my last post, I wrote about using the Shapley Value to divide a coalition’s payoffs among its members and analyze it for its most valuable members. In today’s post I will discuss the stability of these coalitions.

Coalitions are not always stable. In a cooperative game, players can defect to act on their own or create sub-coalitions through which they may get higher payoffs. Brexit and the Soviet collapse are exemplars of constituent states breaking out of a union because they see a higher payoff alone than in the union. Rearrangement of coalitions are, in fact, ubiquitous.

• Adolescents move out of their parents’ house for a higher degree of freedom

• Students who do not see value in a college education drop out to learn by themselves.

• People change jobs when they feel that they can create and extract more value in another organization.

• Immigrants move across continents for better opportunities.

• Political groups break into multiple factions after major disagreements.

Individual Payoffs

Individual payoffs are the key factors that decide whether a coalition is stable or not. At times, ever after a completely fair division, some players end up getting a lower payoff than they might have received alone or in another coalition. These players will want to defect from the coalition.

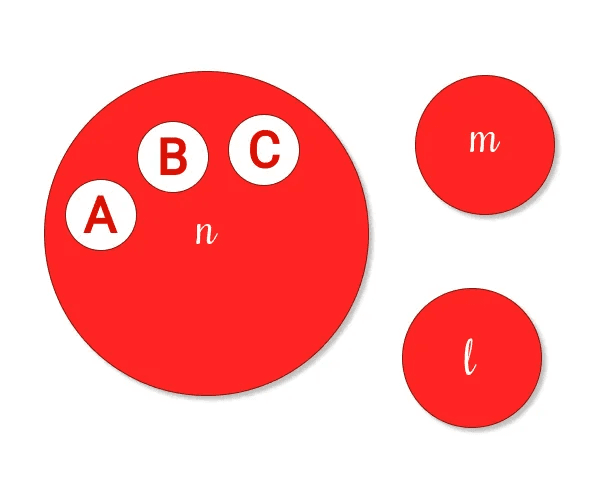
Let’s take a group of 3 people, where A is the set of available actions to Alice, B for Bob, and C for Carol. The payoffs for each action for each player are the same and are in the order of l < m < n.

A = [ l, m, n ] B = [ l, m, n ] C = [ m, n ]

The group will choose go ahead with n as it gives all of them the highest payoff among available options.

If we introduce a new action o that has a payoff higher than all existing actions and make it available to only Bob and Carol, the new action sets are

A = [ l, m, n ] B = [ l, m, n, o ] C = [ m, n, o ]

To act in unison, the players need to choose between options m and n. The group cannot choose o because it is not available to Alice. Here, Bob and Carol will form a sub-coalition to choose the action o and Alice will be left alone to choose n. In this case, the players are incentivized not to act in unison which makes the grand coalition unstable.

If Alice wants Bob and Carol to form a coalition with her, she will have to offer them a redistribution of payoffs in a way that results in the individual payoffs for both Bob and Carol being higher than or at least equal to the payoffs than when they choose o in their sub-coalition. Such a redistribution of payoffs results in Alice getting a lower payoff than she would alone and therefore she should not offer it.

In the real world, however, we often make misguided, irrational or even unlucky decisions that result in such unreasonable division of payoffs. These decisions are usually followed by a sour experience. Some examples that come to mind are

• paid internship programs where students pay to get work experience

• startups joining paid accelerators and incubators for exposure

• countries falling into Chinese debt traps

Creating Stability

Stability in a coalition boils down to determining at least one way of dividing the payoffs under which every player would want to form that coalition over every other coalition.

A feasible and efficient payoff is a precondition for stability. A feasible payoff does not distribute more than the worth of the coalition. An efficient payoff is a feasible payoff that distributes the total worth of the coalition. While games can be stable with inefficient payoffs, an efficient payoff for the same game improves upon the individual payoffs of the players making it more stable.

The recent fair-launch of the YFI Token in which its creator did not take any pre-mined tokens improved the payoffs for the game’s participants and improved the likelihood of player participation. The token’s success speaks for itself.

The Core

To achieve stability in a cooperative game, each player must be incentivized to form the grand coalition, which is a coalition of all the players in a game. In game theory, the core is the set of efficient allocations that cannot be improved upon by a sub-coalition of the game’s players. The core can be empty or contain multiple payoff vectors. Any payment profiles drawn from the core makes the grand coalition stable.

Caution or Rejoice. Math ahead.

A cooperative game G is defined by (N, v) where N is the set of all players in the game and v is the characteristic function that that maps each coalition S ⊆ N to its worth v(S). We assume that v(∅) = 0.

A payoff vector x is in the core of a cooperative game (N, v) if and only if

Let's consider a game G = (N, v) where N = [ A, B, C ] and the characteristic function v given as follows: v(∅) = 0 v({A}) = 2 v({B}) = 1 v({C}) = 2 v({A, B}) = 5 v({B, C}) = 4 v({A, C}) = 6 v({A, B, C}) = 10

We can represent the core in a set of payoff vectors or a set of inequalities.

Let x, y, z be the respective payoffs for A, B, C in the grand coalition.

For our payoff division to be feasible and efficient, the sum of the payoffs should be equal to the worth of the grand coalition. Our first pre-condition comes out to be

• x + y + z = 10

For our payoff division to be individually rational, the players should get a better payoff by participating in the game than not. Our first set of inequalities come out to be

• x ≥ 2

• y ≥ 1

• z ≥ 2

For our payoff division to be group rational, the players should get a better payoff in the grand coalition than in other coalitions. Our second set of inequalities come out to be

• x + y ≥ 5

• y + z ≥ 4

• x + z ≥ 6

The Core of Game G where x, y and z are the respective payoffs of A, B and C is represented by the following conditions x+y+z = 10 x ≥ 2, y ≥ 1, z ≥ 2 x+y ≥ 5, y+z ≥ 4, x+z ≥ 6

Visual Representation of the Core

Our 3 player game can be visualized in a simplex plot of x+y+ z = 10 where the inequalities x ≥ 2, y ≥ 1, z ≥ 2 form the sides of a triangle. The area of the triangle cut by the remaining inequalities x+y ≥ 5, y+z ≥ 4, x+z ≥ 6 is the core.

All points that fall within the core, including points on its edges, represent stable payoff divisions. In this game, the points (2,3,5), (2,4,4), (3,2,5), (3,3,4), (3,4,3), (4,1,5), (4,2,4), (4,3,3), (4,4,2), (5,1,4), (5,2,3), (5,3,2), (6,1,3) and (6,2,2) fall within the core. Any of the payoffs represented by these points will result in a stable grand coalition. In case the core is empty, the grand coalition will be unstable and break into smaller groups.

Applications

Our minds respond to incentives and all our conscious decisions are made considering their perceived payoffs. Although a simple concept, its impact on human behavior is astoundingly high.

Incentivizing Public Transport

In many places people prefer to travel by car over public transport. When thousands of cars come out on the streets, they create congestion and gridlocks, drive up energy consumption, and contribute to air pollution. Cities interested in incentivizing public transport can leverage the core to create a set of incentives such that using public transport becomes the obvious choice for a majority of the population.

Team Dynamics and Employee Retention

Team leaders such as CEOs and Product Leads should understand the individual goals of all their team members and use simple math to find the core and create astonishingly high levels of coordination in their teams. Companies can also use the core to determine salaries, stock options and many other job perks for their employees that aim to subdue their temptations of leaving their jobs.

It also explains why certain executives and managers get absurdly high salaries which does not seem to reflect their contribution. They are not paid to work but instead not to leave.

Immigration and Brain Drain

For decades, the United States has been the prime destination for immigrants seeking a better life. That is rapidly changing as other developed countries in need of skilled workers are coming up with policies to attract talented young individuals. Germany’s next-to-zero college tuition attracts students from around the world who later decide to stay for a job. Canada and Australia welcome immigrants with a fast immigration process for skilled workers. On the other end of the spectrum, developing countries like India are trying to prevent brain drain by incentivizing the youth to stay and contribute to the local economy. All these countries could use the core and other concepts from cooperative game theory to their benefit.