A Lesson in the Babylonian Talmud

The Babylonian Talmud is a collection of ancient texts that document and interpret Jewish law. The following problem appeared in a mishna from the 2000 year old talmud.

Two hold a garment; one claims it all, the other claims half.
How should the garment be fairly divided?

A logical answer would be to divide the piece of cloth in a way that each claimant gets a share proportional to its claim, which leads to the first claimant getting 2/3rd of the garment and the second claimant the remaining 1/3rd.

In the real world however, it is common to see aggressive claimants ending up with significantly bigger pieces than what seems fair. Why does it happen in such a way?

For answers, we turn back to the talmud, which states that the one who claims it all gets three-fourths of the garment and the other who claims half gets the remaining fourth. Another instance of fair division in the talmud states that where one claims all, and another claims a third, he who claims all gets five-sixths and the other a sixth. This division, while hardly seems fair, has a strong logical basis. The person who claims only half the cloth has already conceded the other half to his opponent, and only half of the garment remains contested. In the absence of a legible proof of ownership, a fair and equal division of the contested half results in the aforementioned split. Similarly, in the second case, only a third of the estate is disputed, which gets equally split and divided among the two.

To define this practice of fair division in the talmud, we have coined the Contested Garment Rule as follows:

-

Let two individuals have claims against a common asset, where the sum of the claims exceed or are equal to the total amount. Each claimant’s uncontested portion is the amount left over after the other claimant has been paid in full in case that claim is less than the total, and zero otherwise. The contested garment rule gives each claimant their uncontested portion plus one-half of the excess over and above the sum of the uncontested portions.

-

The Contested Garment Rule derived from the Babylonian talmud helps us understand the concept of fair division and is leveraged in many modern day scenarios.

Corporate Negotiation Tactics

We learn from the contested garment rule that if one wishes to split something in half, one should lay complete claim to it. Claiming the entire pie puts everything on the negotiating table and concedes nothing to the other player.

In corporate negotiations such as mergers and acquisitions, companies know that an even split of the pie would seem fair and to maximize their payoffs, they claim much higher valuations than they would settle for.

Chinese Territorial Disputes

The Chinese are smart and understand fair division in conflict resolution. The Communist Party of China has a history of making unprecedented territorial claims. In 1950, China laid claim to Tibet and invaded the region. Today, China claims sovereignty over Taiwan, has disputed borders with India, lays administrative claim to the autonomous region of Hong Kong, and frequently plays the role of an aggressor in the South China Sea.

Beijing’s strategy of territorial disputes is a simple one to understand - If you have a neighbor that is unlikely to go to war, claim their territory. After a peaceful resolution, your expected payoff is precisely half of the disputed territory.

The Shapley Value

In a real world scenario, there may be more than two contestants for a disputed property. In such cases, calculating an even split can get complex with every new player. For fair division among three or more players, we can use the Shapley value to split the contested property.

In game theory, the Shapley value is a solution concept of fairly distributing both gains and costs to several actors working in a coalition. Mathematically, the Shapley value is the average expected marginal contribution of one player after all possible combinations have been considered.

Calculating the Shapley Value

The Shapley value is calculated by averaging over all orderings, the payoff of each player when the contested property is claimed in a first-come-first-serve manner.

When 3 individuals A, B and C respectively claim a share of $100, $200 and $300 in an asset worth $500. The first-come-first-serve orderings are as follows:

Here, the average values across multiple orderings (or the Shapley values) add up to the asset value of $500, and can be regarded as an even split of the pie.

We can also use Shapley value calculations for claims between two people. It is interesting to observe that Shapley values of the two players are consistent with the split proposed in the talmud.

Talmud Case 1

When 2 individuals A and B respectively claim a share of $100 and $50 in an asset worth $100. The first-come-first-serve orderings are as follows:

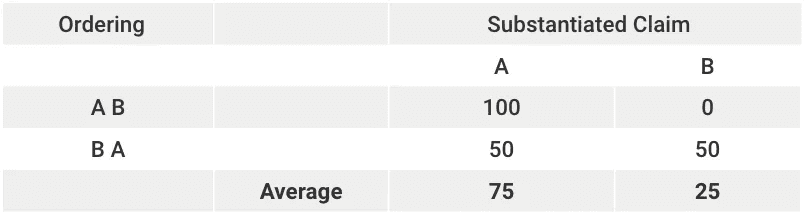
The computed Shapley values of $75 for A and $25 for B are consistent with the 3:1 split proposed in the talmud.

Talmud Case 2

When 2 individuals A and B respectively claim a share of $100 and $33.33 in an asset worth $100. The first-come-first-serve orderings are as follows:

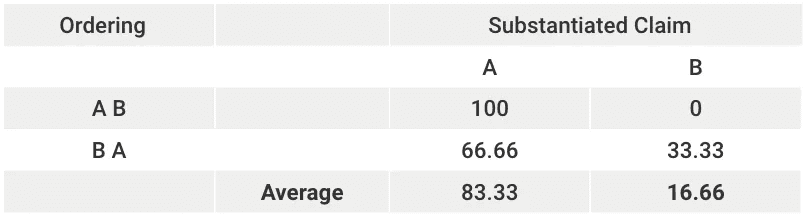
The computed Shapley values of $83.33 for A and $16.66 for B are consistent with the 5:1 split proposed in the talmud.

Calculating Shapley values can resolve complex problems like estate division, profit distribution and priority allocation.

Bankruptcy Cases

When an entity defaults on its loans, creditors come looking for blood. In bankruptcy cases, the defaulter’s liabilities outweigh the defaulter’s assets. How do five creditors split the assets in a fair manner? The Shapley value proves to be a useful tool in such cases.

Priority Allocation

In board meetings of large companies, all board members may not see eye-to-eye for a company’s roadmap. When every member has their own list of priorities, the Shapley value for all options may be calculated to assign priorities to the company’s operations.

-

Aristotle once said that quarrels arise when equals are allotted unequal shares, or persons not equal are allotted equal shares. Such quarrels have been going on for a long time and will continue into the future. We will encounter many disputes throughout our life and I wrote this post so we could arm ourselves with the knowledge of fair division.

If you think the concept of fair division and Shapley value has useful applications, share it with a friend who would also find this useful.

-

Further Readings

• H. Peyton Young. Equity: In Theory and Practice

• Robert J. Aumann. Game Theory in the Talmud

• Kevin Leyton-Brown, Yoav Shoham. Essentials of Game Theory: A Concise, Multidisciplinary Introduction

• Anton-Hermann Chroust, David L. Osborn. Aristotle's Conception of Justice